Additive Combinatorics and its Applications in Theoretical Computer Science
Theory of Computing, Graduate Surveys 8, pp. 1-55, 2017
Bibliography with links to cited articles
[1] Noga Alon: Testing subgraphs in large graphs. Random Structures and Algorithms, 21(3-4):359–370, 2002. Preliminary version in FOCS’01. [doi:10.1002/rsa.10056]
[2] Noga Alon, Tali Kaufman, Michael Krivelevich, Simon Litsyn, and Dana Ron: Testing Reed-Muller codes. IEEE Trans. Inform. Theory, 51(11):4032–4039, 2005. Preliminary version in RANDOM’03. [doi:10.1109/TIT.2005.856958]
[3] Antal Balog and Endre Szemerédi: A statistical theorem of set addition. Combinatorica, 14(3):263–268, 1994. [doi:10.1007/BF01212974]
[4] Boaz Barak, Russell Impagliazzo, and Avi Wigderson: Extracting randomness using few independent sources. SIAM J. Comput., 36(4):1095–1118, 2006. Preliminary version in FOCS’04. [doi:10.1137/S0097539705447141]
[5] Boaz Barak, Anup Rao, Ronen Shaltiel, and Avi Wigderson: 2-source dispersers for sub-polynomial entropy and Ramsey graphs beating the Frankl-Wilson construction. In Proc. 38th STOC, pp. 671–680. ACM Press, 2006. [doi:10.1145/1132516.1132611]
[6] Boaz Barak, Luca Trevisan, and Avi Wigderson: A mini-course on additive combinatorics, 2007. Available at course website.
[7] Michael Bateman and Nets Katz: New bounds on cap sets. J. Amer. Math. Soc., 25(2):585–613, 2012. [doi:10.1090/S0894-0347-2011-00725-X, arXiv:1101.5851]
[8] Felix A. Behrend: On sets of integers which contain no three terms in arithmetical progression. Proc. Nat. Acad. Sci. U.S.A., 32(12):331–332, 1946. Available at PMC.
[9] Mihir Bellare, Don Coppersmith, Johan Håstad, Marcos Kiwi, and Madhu Sudan: Linearity testing over characteristic two. IEEE Trans. Inform. Theory, 42(6):1781–1795, 1996. Preliminary version in FOCS’95. [doi:10.1109/18.556674]
[10] Eli Ben-Sasson, Shachar Lovett, and Noga Ron-Zewi: An additive combinatorics approach relating rank to communication complexity. J. ACM, 61(4):22:1–22:18, 2014. Preliminary versions in FOCS’12 and ECCC. [doi:10.1145/2629598]
[11] Eli Ben-Sasson and Noga Ron-Zewi: From affine to two-source extractors via approximate duality. SIAM J. Comput., 44(6):1670–1697, 2015. Preliminary versions in STOC’11 and ECCC. [doi:10.1137/12089003X]
[12] Abhishek Bhowmick, Zeev Dvir, and Shachar Lovett: New bounds for matching vector families. SIAM J. Comput., 43(5):1654–1683, 2014. Preliminary versions in STOC’13 and ECCC. [doi:10.1137/130932296]
[13] Khodakhast Bibak: Additive combinatorics with a view towards computer science and cryptography – an exposition. In Number Theory and Related Fields, volume 43, pp. 99–128. Springer, 2013. [doi:10.1007/978-1-4614-6642-0_4, arXiv:1108.3790]
[14] Thomas F. Bloom: Translation invariant equations and the method of Sanders. Bull. London Math. Soc., 44(5):1050–1067, 2012. [doi:10.1112/blms/bds045, arXiv:1107.1110]
[15] Manuel Blum, Michael Luby, and Ronitt Rubinfeld: Self-testing/correcting with applications to numerical problems. J. Comput. System Sci., 47(3):549–595, 1993. Preliminary version in STOC’90. [doi:10.1016/0022-0000(93)90044-W]
[16] Jean Bourgain: On triples in arithmetic progression. Geom. Funct. Anal., 9(5):968–984, 1999. [doi:10.1007/s000390050105]
[17] Jean Bourgain: More on the sum-product phenomenon in prime fields and its applictaions. Internat. J. Number Theory, 1(1):1–32, 2005. [doi:10.1142/S1793042105000108]
[18] Jean Bourgain: Roth’s theorem on progressions revisited. Journal d’Analyse Mathématique, 104(1):155–192, 2008. [doi:10.1007/s11854-008-0020-x]
[19] Jean Bourgain, Aleksei A. Glibichuk, and Sergei Vladimirovich Konyagin: Estimates for the number of sums and products and for exponential sums in fields of prime order. J. London Math. Soc., 73(2):380–398, 2006. [doi:10.1112/S0024610706022721]
[20] Jean Bourgain, Nets Katz, and Terence Tao: A sum-product estimate in finite fields, and applications. Geom. Funct. Anal., 14(1):27–57, 2004. [doi:10.1007/s00039-004-0451-1, arXiv:math/0301343]
[21] Mei-Chu Chang: Some consequences of the polynomial Freiman–Ruzsa conjecture. C. R. Acad. Sci. Paris Ser. I Math., 347(11-12):583–588, 2009. [doi:10.1016/j.crma.2009.04.006]
[22] Stephen A. Cook: The complexity of theorem-proving procedures. In Proc. 3rd STOC, pp. 151–158. ACM Press, 1971. [doi:10.1145/800157.805047]
[23] Ernie Croot, Vsevolod F. Lev, and Péter Pál Pach: Progression-free sets in Z4n are exponentially small, 2016. [arXiv:1605.01506]
[24] Holger Dell and Dieter van Melkebeek: Satisfiability allows no nontrivial sparsification unless the polynomial-time hierarchy collapses. J. ACM, 61(4):23:1–23:27, 2014. Preliminary version in STOC’10. [doi:10.1145/2629620]
[25] Jean-Marc Deshouillers, François Hennecart, and Alain Plagne: On small sumsets in (Z∕2Z)n. Combinatorica, 24(1):53–68, 2004. [doi:10.1007/s00493-004-0004-0]
[26] György Elekes: On the number of sums and products. Acta Arithm., 81(4):365–367, 1997.
[27] Jordan S. Ellenberg and Dion Gijswijt: On large subsets of Fqn with no three-term arithmetic progression, 2016. [arXiv:1605.09223]
[28] Paul Erd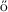 s and Endre Szemerédi: On
sums and products of integers. Studies in Pure Math., pp. 213–218, 1983.
[doi:10.1007/978-3-0348-5438-2_19]
s and Endre Szemerédi: On
sums and products of integers. Studies in Pure Math., pp. 213–218, 1983.
[doi:10.1007/978-3-0348-5438-2_19]
[29] Chaim Even-Zohar: On sums of generating sets in Z2n. Combin. Probab. Comput., 21(6):916–941, 2012. [doi:10.1017/S0963548312000351, arXiv:1108.4902]
[30] Chaim Even-Zohar and Shachar Lovett: The Freiman–Ruzsa theorem over finite fields. J. Combinat. Theory, Ser. A, 125:333–341, 2014. Preliminary verion in ECCC. [doi:10.1016/j.jcta.2014.03.011, arXiv:1212.5738]
[31] Jacob Fox: A new proof of the graph removal lemma. Ann. of Math., 174(1):561–579, 2011. [doi:10.4007/annals.2011.174.1.17, arXiv:1006.1300]
[32] Gregory Abelevich Freiman: Foundations of a structural theory of set addition. Volume 37. Amer. Math. Soc., 1973.
[33] Oded Goldreich: Introduction to testing graph properties. In Property Testing, volume 6390 of LNCS, pp. 105–141. Springer, 2010. [doi:10.1007/978-3-642-16367-8_7]
[34] William Timothy Gowers: A new proof of Szemerédi’s theorem. Geom. Funct. Anal., 11(3):465–588, 2001. [doi:10.1007/s00039-001-0332-9]
[35] Ben J. Green: Finite field models in additive combinatorics. Surveys in Combinatorics, pp. 1–28, 2005. [doi:10.1017/CBO9780511734885.002, arXiv:math/0409420]
[36] Ben J. Green: The polynomial Freiman-Ruzsa conjecture, 2005. Available at author’s website.
[37] Ben J. Green: The polynomial Freiman-Ruzsa conjecture. Open Problems in Math., 2:1–3, 2014.
[38] Ben J. Green and Terence Tao: The primes contain arbitrarily long arithmetic progressions. Ann. of Math., 167(2):481–547, 2008. [doi:10.4007/annals.2008.167.481, arXiv:math/0404188]
[39] Ben J. Green and Terence Tao: Freiman’s theorem in finite fields via extremal set theory. Combin. Probab. Comput., 18(3):335–355, 2009. [doi:10.1017/S0963548309009821, arXiv:math/0703668]
[40] David Rodney Heath-Brown: Integer sets containing no arithmetic progressions. J. London Math. Soc., s2-35(3):385–394, 1987. [doi:10.1112/jlms/s2-35.3.385]
[41] Alex Iosevich, Oliver Roche-Newton, and Misha Rudnev: On an application of Guth-Katz theorem. Math. Res. Lett., 18(4):691–697, 2011. [doi:10.4310/MRL.2011.v18.n4.a8, arXiv:1103.1354]
[42] Richard M. Karp: Reducibility among combinatorial problems. In Raymond E. Miller and James W. Thatcher, editors, Complexity of Computer Computations, The IBM Research Symposia Series, pp. 85–103. Springer, 1972. [doi:10.1007/978-1-4684-2001-2_9]
[43] Tali Kaufman and Madhu Sudan: Algebraic property testing: the role of invariance. In Proc. 40th STOC, pp. 403–412. ACM Press, 2008. [doi:10.1145/1374376.1374434]
[44] Sergei Vladimirovich Konyagin: A sum-product estimate in fields of prime order, 2003. [arXiv:math/0304217]
[45] Sergei Vladimirovich Konyagin: On the Freiman theorem in finite fields. Math. Notes, 84(3):435–438, 2008. [doi:10.1134/S0001434608090137]
[46] János Körner and Katalin Marton: How to encode the modulo-two sum of binary sources. IEEE Trans. Inform. Theory, 25(2):219–221, 1979.
[47] Izabella Łaba: Fuglede’s conjecture for a union of two intervals. Proc. Amer. Math. Soc., 129(10):2965–2972, 2001. [doi:10.1090/S0002-9939-01-06035-X, arXiv:math/0002067]
[48] Leonid A. Levin: Universal sequential search problems. Problems of Information Transmission, 9(3):115–116, 1973. Available at Mathnet.
[49] Shachar Lovett: An exposition of Sanders’ quasi-polynomial Freiman-Ruzsa theorem. Number 6 in Graduate Surveys. Theory of Computing Library, 2015. Preliminary version in ECCC. [doi:10.4086/toc.gs.2015.006]
[50] Roy Meshulam: On subsets of finite abelian groups with no 3-term arithmetic progressions. J. Combinat. Theory, Ser. A, 71(1):168–172, 1995. [doi:10.1016/0097-3165(95)90024-1]
[51] Giorgis Petridis: New proofs of Plünnecke-type estimates for product sets in groups. Combinatorica, 32(6):721–733, 2012. [doi:10.1007/s00493-012-2818-5, arXiv:1101.3507]
[52] Helmut Plünneke: Eigenschaften und Abschätzungen von Wirkungsfunktionen. Gesellschaft für Mathematik und Datenverarbeitung, 1969.
[53] Robert Alexander Rankin: Sets of integers containing not more than a given number of terms in arithmetical progression. Proc. Royal Soc. Edinburgh. Sec. A. Math. Phys. Sci., 65(4):332–344, 1961. [doi:10.1017/S0080454100017726]
[54] Anup Rao: An exposition of Bourgain’s 2-source extractor. Electronic Colloquium on Computational Complexity (ECCC), 14(34), 2007. ECCC.
[55] Klaus Roth: Sur quelques ensembles d’entiers. C. R. Acad. Sci. Paris Ser. I Math., 234:388–390, 1952.
[56] Klaus Roth: On certain sets of integers. J. London Math. Soc., s1-28(1):104–109, 1953. [doi:10.1112/jlms/s1-28.1.104]
[57] Ronitt Rubinfeld and Madhu Sudan: Robust characterizations of polynomials and their applications to program testing. SIAM J. Comput., 25(2):252–271, 1996. [doi:10.1137/S0097539793255151]
[58] Imre Z. Ruzsa: Arithmetical progressions and the number of sums. Periodica Math. Hung., 25(1):105–111, 1992. [doi:10.1007/BF02454387]
[59] Imre Z. Ruzsa: An analog of Freiman’s theorem in groups. Structure Theory of Set-Addition. Astérisque, 258:323–326, 1999. Available at author’s website. Virtually identical version available as DIMACS TR 93-77, 1993 from CiteSeer.
[60] Imre Z. Ruzsa and Endre Szemerédi: Triple systems with no six points carrying three triangles. In Coll. Math. Soc. J. Bolyai, volume 18, pp. 939–945. Bolyai Soc. and North-Holland, 1978.
[61] Alex Samorodnitsky: Low-degree tests at large distances. In Proc. 39th STOC, pp. 506–515. ACM Press, 2007. [doi:10.1145/1250790.1250864, arXiv:math/0604353]
[62] Tom Sanders: A note on Freiman’s theorem in vector spaces. Combin. Probab. Comput., 17(2):297–305, 2008. [doi:10.1017/S0963548307008644, arXiv:math/0605523]
[63] Tom Sanders: On Roth’s theorem on progressions. Ann. of Math., 174(1):619–636, 2011. [doi:10.4007/annals.2011.174.1.20, arXiv:1011.0104]
[64] Tom Sanders: On certain other sets of integers. Journal d’Analyse Mathématique, 116(1):53–82, 2012. [doi:10.1007/s11854-012-0003-9, arXiv:1007.5444]
[65] Tom Sanders: On the Bogolyubov-Ruzsa lemma. Analysis and PDE, 5(3):627–655, 2012. [doi:10.2140/apde.2012.5.627, arXiv:1011.0107]
[66] Igor E. Shparlinski: Additive combinatorics over finite fields: New results and applications. In Finite Fields and Their Applications: Character Sums and Polynomials, volume 11 of Radon Series on Computational and Applied Mathematics, pp. 233–272. De Gruyter, 2013.
[67] József Solymosi: Bounding multiplicative energy by the sumset. Advances in Math., 222(2):402–408, 2009. [doi:10.1016/j.aim.2009.04.006, arXiv:0806.1040]
[68] Benny Sudakov, Endre Szemerédi, and Van H. Vu: On a question
of Erd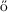 s and Moser. Duke Math. J., 129(1):129–155, 2005.
[doi:10.1215/S0012-7094-04-12915-X]
s and Moser. Duke Math. J., 129(1):129–155, 2005.
[doi:10.1215/S0012-7094-04-12915-X]
[69] László A. Székely: Crossing numbers and hard erd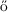 s problems in
discrete geometry. Combinatorics, Probability and Computing, 6(3):353358,
1997. [doi:10.1017/S0963548397002976]
s problems in
discrete geometry. Combinatorics, Probability and Computing, 6(3):353358,
1997. [doi:10.1017/S0963548397002976]
[70] Endre Szemerédi: On sets of integers containing no k elements in arithmetic progression. Acta Arithmetica, 27(1):199–245, 1975. Available at PLDML.
[71] Endre Szemerédi: Integer sets containing no arithmetic progressions. Acta Math. Hung., 56(1):155–158, 1990. [doi:10.1007/BF01903717]
[72] Endre Szemerédi and William T. Trotter: Extremal problems in discrete geometry. Combinatorica, 3(3-4):381–392, 1983. [doi:10.1007/BF02579194]
[73] Terence Tao and Van H. Vu: Additive Combinatorics. Volume 13. Cambridge Univ. Press, 2006.
[74] Luca Trevisan: Additive combinatorics and theoretical computer science. ACM SIGACT News, 40(2):50–66, 2009. [doi:10.1145/1556154.1556170]
[75] Emanuele Viola: Selected Results in Additive Combinatorics: An Exposition. Number 3 in Graduate Surveys. Theory of Computing Library, 2011. [doi:10.4086/toc.gs.2011.003]
[76] Bartel Leendert van der Waerden: Beweis einer Baudetschen Vermutung. Nieuw Arch. Wisk., 15:212–216, 1927.
